私たちは地球が、惑星が、太陽の周囲を回っていることを知っていますが、地球のうえにいてそれを直感的に確認するのは困難です。地球という自分の視点から周囲が動く様子をみて、自分が中心だと考えるのはごく自然なことなので、歴史的には天動説と地動説という流れが生じました。

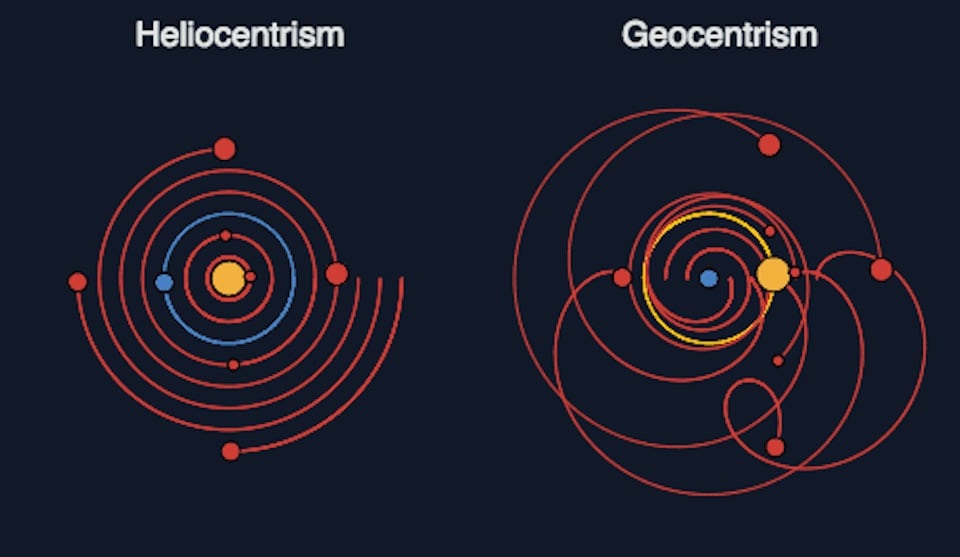
これを端的に表現するアニメーションが、太陽を中心した場合の惑星の動きと、地球を中心にした場合の太陽と惑星の動きを比較していて理解しやすく、みていて吸い込まれるようでした。

同じ現象を、座標変換して見る

本当は鉛筆舐めてちゃんと数式を書いておけば良いのですが、ちょっと時間がないですし知っている人には簡単に導出できる話ですので、ここでは「どうやって描いているの？」という方向けに入り口だけ。

この二つの画像のうち、左はわかりやすくて、単に同心円をそれぞれの惑星のスピードに合わせて描いているだけです。正確には惑星は同心円ではなく楕円軌道ですが、まあそれはそれ。右はどうなっているのでしょう？

太陽を中心にして描くとそれぞれの惑星について距離と角度がありますが、それを地球を中心にした座標系に変換するということをしています。実際に地球上にいた場合、距離の変化は概ね明るさとして、角度は黄道上の場所として体感できます。

地球の動きに対して外惑星はゆっくりと動きますから、地球上でみたときには見かけ上の逆行が生じていて、そのせいで右側は非常に複雑にみえるのですね。

このアニメーションの美しいのは、描いているのは同じ現象なのに、視点を変えるだけでこれだけ違って見えること、そしてそれは数学的には単に座標変換として表現できる点です。べつに、地球のまわりにすべてが回転していると言ってもいいのです。でも地球中心の座標系で惑星の移動を表現するのに比べて、太陽中心にしたほうがなんとすっきりすることか。

細かい話をいうと、正確にはこれは地動説・天動説には対応しておらず、太陽中心の座標系と地球中心座標系の違いを表現したアニメーションなのですが、まあおおまかな説明としてはそれで通じるかと。

このたった一枚の画像に、プラトンやアリストテレス、プトレマイオスから、コペルニクス、ケプラー、ガリレオにいたる人間の視座の獲得があると言ってもよいのですが、そう考えると、私たちの知ってることとというのは、いかに多くの人々によって描かれ、描き直されて進歩したのかということにも思いを馳せずにいられません。

もともとのアニメーションを作成したMalin Christerssonさんのサイトには、三角関数の教材としてウェブベースのこうしたアニメーションや、インタラクティブなコンテンツを公開していますので、興味のある方はそちらも御覧ください。

（via Elegance, illustrated: heliocentrism vs geocentrism | Boing Boing)